Projected health impact of post-discharge malaria chemoprevention among children with severe malarial anaemia in Africa

Post-discharge cohort model

We initially considered using an existing well-established malaria transmission model to describe the incidence of malaria outcomes post-discharge²². However, preliminary analysis indicated that the high incidence of uncomplicated and hospitalised malaria after a severe malarial anaemia (SMA) episode, as observed in trials and clinical studies^11,17, was not adequately captured using this existing model, despite allowing for individual variation in immunity and exposure to mosquito bites. This is because the model was calibrated against population level incidence data, not against longitudinal data on risk within individuals over time. For the current analysis, a novel model was created to describe the natural history of malaria illness in the post-discharge population, how it changes over time and with varying malaria transmission intensities.

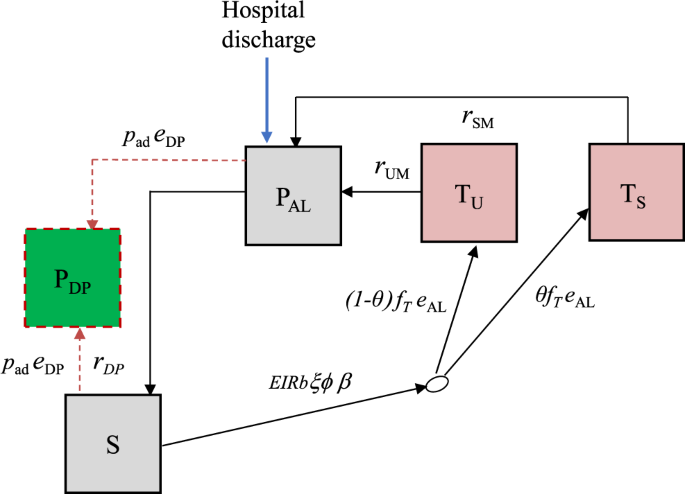
We developed a deterministic, discrete-time compartmental model with the following states: prophylaxis (P_DP and P_AL), susceptible (S), treated uncomplicated malaria (T_U), and treated hospitalised malaria (T_S) (Fig. 4).

Boxes represent health states, while arrows and labels show health state transition rates and probabilities of an event. Definitions are given in the text and Table S1. See supplementary information for further details.

Children are given artemether-lumefantrine (AL) at the time of hospital discharge to clear any remaining malaria parasites, which provides a period of prophylaxis against reinfection. Therefore, children enter the model into the protected state \({P}_{{{{{{\rm{AL}}}}}}}\) on the first day of their treatment. We modelled this initial period of AL protection as gamma-distributed with an average of 13 days based on previous analysis of reinfection during clinical trials of AL³⁶. After prophylaxis, children in the placebo group enter the susceptible state \(S\) and experience symptomatic malaria (uncomplicated or hospitalised) at a rate equal to the product of the local entomological inoculation rate (EIR), the probability that an infectious bite leads to infection b, the probability of symptoms ϕ and the relative exposure to bites among the post-discharge group of children ξ compared to the average child (Table S1). We only observe the incidence of symptomatic malaria, so these parameters are not individually identifiable and during model fitting, we estimate them as a product \(b{\phi }{\xi }\). We assume that each infectious bite can only cause one symptomatic episode. Upon developing symptoms, we allowed a two-day delay for treatment seeking. Uncomplicated cases enter state \({T}_{U}\) and then go on to receive AL treatment which has 98% efficacy⁵ and provides 13 days of prophylaxis (state \({P}_{{{{{{\rm{AL}}}}}}}\)). A proportion θ of symptomatic malaria cases experience disease sufficiently severe to be readmitted to hospital (they need parenteral antimalarials or have severe malarial anaemia), and enter a treated severe state \({T}_{S}\) which includes a mean hospital stay of 3 days based on the trial data¹¹. As before, AL is then given at discharge, and the children enter state \({P}_{{{{{{\rm{AL}}}}}}}\). Hospitalised cases include those who meet the strict WHO case definition of severe malaria as well as those who do not²⁷, in line with the outcome metric in the PDMC trial used for fitting the model¹¹. We assumed that all uncomplicated and severe malaria episodes during follow-up were detected and treated. This is a reasonable assumption because the trial reimbursed participant costs of treatment seeking at study clinics, diminishing financial barriers to care. We do not track asymptomatic infections and those infected without symptoms remain in the S state, which represents those susceptible to clinical malaria disease.

We further allow that the risk of symptomatic malaria per infectious bite could decline over time since hospital discharge, based on results from the PDMC trial, other post-discharge studies, and the hypothesis that recovery will reduce vulnerability^8,11. We estimated the rate of the decline by allowing total incidence in the cohort to be scaled by a Weibull survival curve:

where \({t}_{d}\) is the time since hospital discharge and the scale and shape parameters \({{\lambda }}_{{{{{{\rm{risk}}}}}}}\) and \({{\eta }}_{{{{{{\rm{risk}}}}}}}\), are estimated.

The average probability that an infectious bite leads to successful infection and then to symptoms are both known to decline with increasing transmission intensity in the general population in any given setting due to acquired immunity and density-dependent effects, e.g. competition between parasites. We included this possibility by further scaling total incidence in each location by a similar functional form to that identified in previous analyses^15,37 of the relationship of EIR and the probability of symptomatic malaria:

and estimated the parameter \(w\), since the relationship is unknown in this post-discharge population.

We track children in the PDMC trial arm separately. The model describing these children is the same as the placebo group except for additional PDMC protection against uncomplicated and hospitalised episodes. PDMC is given as three full courses of dihydroartemisinin-piperaquine (DP) starting at the beginning of weeks 2, 6 and 10 post-discharge. We modelled DP prophylaxis as a probability of prevention of reinfection that declines over time since treatment, using a Weibull-survival function as in previous work:³⁶

where t_DP is the time since the last PDMC treatment, and \({{\lambda }}_{{{{{{\rm{DP}}}}}}}\) and \({{\eta }}_{{{{{{\rm{DP}}}}}}}\) represent the scale and shape parameters of the Weibull distribution. We allowed for different adherence to each of the three courses of PDMC based on trial data when fitting to the trial (Table 1, main text). For simplicity, we assumed that for each course of PDMC, caregivers either gave all three doses or none, which was relatively consistent with observations during implementation (only 1.5% of children received 1–2 doses of DP per treatment course, with the remainder taking all or none)²³. The DP protection is applied to all children in the PDMC intervention group, except children in states \({T}_{U}\), \({T}_{S}\) and \({P}_{{{{{{\rm{AL}}}}}}}\) (currently symptomatic and treated). When children leave the \({T}_{U}\) and \({T}_{S}\) states and return to S, we assume they have the same protection as those who did take PDMC. This approximately captures the trial recommendation that children should take PDMC once recovered from their symptomatic episode³⁸, although it was not possible to explicitly include multiple PDMC timings outside the standard trial times due to computational constraints. We further explored whether current PDMC drug protection could reduce the probability of needing hospitalisation, θ . We defined ‘current drug protection’ as inhibitory drug levels providing >1% probability of protection.

Model fitting and validation

We fitted the model to the trial data described above using Bayesian methods. Semi-informative priors for the EIR in each hospital catchment area were based on the Malaria Atlas Project (MAP) estimates of transmission intensity within 20 km of the hospital location (Table S1)¹⁴. We ran the model for each site and fitted to the daily incidence of uncomplicated and hospitalised malaria simultaneously across sites over the 6 months of follow-up. Since hospitalised malaria numbers were small in some sites, this method borrows information from the uncomplicated malaria cases to inform the posterior EIR. The parameters estimated during fitting were: the maximum incidence of symptomatic malaria (uncomplicated and hospitalised) per infectious bite at the beginning of post-discharge follow-up, the EIR in each site, the risk of hospitalised and uncomplicated malaria per infectious bite over time since discharge and with increasing EIR, and the effect of PDMC on severity of illness. All parameters except for EIR were given uninformative priors (Table S1). We coded the model with a timestep of one day, with transition rates converted to daily probabilities. The model was fitted using Markov chain Monte Carlo methods in the RStan software³⁹. We ran four chains, each having 5000 burn-in and 10,000 sampling iterations. We assessed convergence through visualisation of posterior distributions and the Gelman-Rubin’s convergence diagnostic⁴⁰. Full mathematical details of the models, parameters, and fitting procedures are given in the Supplementary Information.

Population modelling of PDMC demand and impact in different epidemiological settings

We next developed a full population model which tracks SMA in all under five year olds (Figure S3), and included the post-discharge cohort model within this framework (see also Supplementary Information). This deterministic model was similarly coded in discrete time. Children are stratified into two risk groups: those who experienced SMA within the last 6 months (high-risk) and those who did not (low-risk). When an episode of SMA occurs in low-risk individuals, they move to the high-risk state. The fitted post-discharge cohort model placebo arm was used to describe the incidence of malaria episodes in the high-risk group in the absence of PDMC, including SMA episodes. Using estimated total SMA incidence for a given area (see sources in the Results section), the remaining SMA episodes occurring in the low-risk group are calculated. In contrast to the model fitted to the trial setting, we assume the probability of children receiving treatment for uncomplicated episodes or being hospitalised when required is <100% (Table S1). We track SMA cases who are hospitalised separately from those who are not. We vary the assumed probability of hospitalisation from 30–70% based on the recent CARAMAL study tracking children with suspected severe malaria in community settings²⁴. We assume that the probability of hospitalisation is not related to previous hospitalisation status. Those who are hospitalised have a fixed 3-day stay in hospital, then we assume that all who survive receive AL at discharge as per standard severe malaria guidelines. Hospitalised SMA cases are eligible for PDMC. PDMC with DP is incorporated as in the post-discharge cohort model, except that adherence is lower as measured in a recent PDMC implementation study²³ (Table S2). We also further stratify the model compartments in children given PDMC to track which courses of PDMC have been taken (any combination of the 1st, 2nd and 3rd courses). After the 6-month high-risk period, individuals return to the low-risk group unless they experience a further episode of SMA. This model thus allows for the iterative process of SMA episodes increasing the risk of future SMA episodes, which affects future PDMC impact and demand. The base case analysis assumes no seasonality in transmission due to uncertainties in the seasonal pattern of SMA cases. To test whether PDMC impact is affected by seasonality, we repeated the analysis assuming that SMA cases follow the same seasonal pattern as EIR (lagged by 15 days to allow for time to symptoms) in each subnational region determined by local rainfall, as established in previous analysis^22,41.

We explicitly model mortality from SMA and from other types of hospitalised malaria during the 25-week post-SMA period. The case fatality rate of SMA in hospital is 7.4% based on a meta-analysis of hospital data²⁶. We allow that only a proportion of other malaria inpatients usually meet the WHO severe malaria case definition criteria²⁷. Since the severity of patients who are hospitalised may vary between settings, we use an in-hospital case fatality rate of 1% based on country reports from Kenya and Uganda, where the trial was carried out^27,42. Of note, this is lower than the case fatality rate of ~9% for hospitalised patients who meet the WHO case definition of severe malaria²⁶. Case fatality rates outside hospital are highly uncertain. We follow the approach of Camponovo et al.²⁷. who triangulated verbal autopsy malaria mortality data in the community with severe malaria incidence. In their analysis the case fatality rate of malaria outside hospital is approximately double that within hospital, and therefore we assume a case fatality rate of 14.8% for non-hospitalised SMA cases and 2% for other cases. In order to keep a constant population size, new individuals are added to the low-risk state at the same rate as the total mortality rate.

The full population model was coded in R and was run to equilibrium, with and without PDMC, to estimate the impact of the intervention. The trials and analyses were approved by the ethics committees at the Kenya Medical Research Institute, Makerere University, the Western Norway Regional Committee for Medical and Health Research Ethics, the Liverpool School of Tropical Medicine, the University of Minnesota, and the Uganda National Council of Science and Technology. Informed consent was originally obtained from parents and guardians.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.